Every electron in an atom can be uniquely identified by a set of four quantum numbers.

Although their discovery required advanced mathematics, they are all conventional numbers: three of them can take only simple integer values; the fourth is a simple fraction.
The first three quantum numbers arise from the wave function, Ψ, obtained by solving the Schrödinger equation.
The fourth quantum number, electron spin, arises from the discovery that electrons have two possible orientations.
The numbers and their definitions are as follows:
The Quantum Numbers
| Quantum Number | Name | Possible Values | Information |
|---|---|---|---|
| n | principal quantum number | 1, 2, 3,..., n | Defines the energy shell occupied by the electron. Shells nearest the nucleus have the lowest value of n and the lowest potential energy.
n is the first number written in electron configurations such as magnesium's: 1s2 2s2 2p6 3s2 |
| l | orbital angular momentum quantum number (also called the azimuthal quantum number) |
0, 1, 2,..., (n-1) | Defines the energy subshell - in systems with more than one electron, the subshells have different energies. l defines the subshell letter in electron configurations. For example: 1s2 2s2 2p6 3s2 l = 0 gives an s subshell. l = 1 gives a p subshell. l = 2 gives a d subshell, etc. |
| ml | magnetic quantum number | -l, (l+1), ..., 0,... , (l+1), l | Defines the orientation of the subshell orbital. The p subshell, with l = 1, has three ml values: -1, 0, 1. These indicate that three p orbitals exist. i.e the orbitals px, py, and pz. The d subshell, with l = 2, has five ml values: -2, -1, 0, 1, 2. These indicate that five d orbitals exist. |
| ms | electron spin quantum number | -½ or +½ | Electrons have two possible spin orientations. |
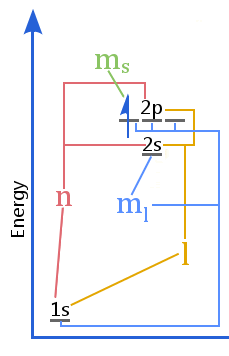
The energy level diagram shows the relationship between quantum numbers vs the shells, subshells, orbitals, and electron spin in an atom.
No electron in an atom shares all four quantum numbers. Every electron can be uniquely identified by its quantum number - see Pauli exclusion principle.
The shapes of orbitals are not given by the quantum numbers, but are probability densities - three dimensional maps of the space around the nucleus where an electron will be found 99 percent of the time. Orbital shapes are obtained from the square of the wave function, Ψ2. The precise location and momentum of any electron can never be known - see Heisenberg uncertainty principle.
