Fundamental particles, such as electrons, may be described as particles or waves.
Electrons may be described using a wave function. The wave function's symbol is the Greek letter psi, Ψ or ψ.

The wave function Ψ is a mathematical expression. It carries crucial information about the electron it is associated with: from the wave function we obtain the electron's energy, angular momentum, and orbital orientation in the shape of the quantum numbers n, l, and ml.
The wave function can have a positive or negative sign. The sign is important in calculations. It is also important when the wave functions of two or more atoms combine to form a molecule.
Wave functions with like signs (waves in phase) will interfere constructively, leading to the possibility of bonding. Wave functions with unalike signs (waves out of phase) will interfere destructively.
In 1926, Erwin Schrödinger deduced the wave function for the simplest of all atoms, hydrogen. Solving the Schrödinger equation enables scientists to determine wave functions for electrons in atoms and molecules.
The Schrödinger equation is an equation of quantum mechanics: calculated wave functions have discrete, allowed values for electrons bound in atoms and molecules; all other values are forbidden.
In addition to the importance of Ψ, its square Ψ2 also has enormous significance in chemistry.
Ψ2 is the probability density. It tells us where the electron is most likely to be found in the space around the nucleus.
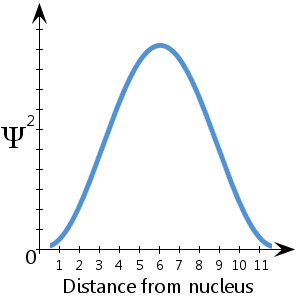
For example, in the (fictitious) schematic diagram plotted here, showing Ψ2 against distance from nucleus, we see that the electron is most likely to be found between about 5-7 units from the nucleus. We also see that there is a vanishingly small likelihood that the electron will be at the nucleus or more than about 11½ units away from the nucleus.
There is a 100 percent probability that the electron is somewhere - in other words a probability of 1.
Ψ can be calculated exactly only for atoms with one electron, i.e. H, He+, Li2+, Be3+, B4+, C5+, etc. In mathematical language, we say that analytic solutions for Ψ are possible only for one-electron systems. One-electron systems are often described as hydrogenic - meaning "like hydrogen."
For all other atoms, ions, and molecules, no analytic solutions for Ψ are possible; approximation methods are necessary to calculate it.
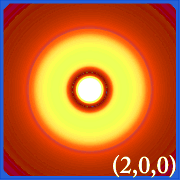
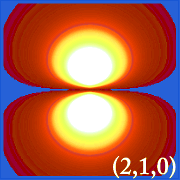
Ψ2 and Hydrogenic Orbitals
Plotting hydrogen's probability density (i.e. Ψ2) for different quantum numbers allows us to visualize the space, centered on the nucleus, that electrons occupy. The various Ψ2 distributions are hydrogen's electron orbitals. The orbital that is actually occupied is determined by the amount of energy the electron has.
Examples of Hydrogen's Orbitals