The orbital approximation is a method of visualizing electron orbitals for chemical species that have two or more electrons.
It does this by modeling a multi-electron atom as a single-electron atom.
The electron of interest feels the individual electric fields of the other electrons and the nucleus.

The electron of interest feels the electric field of the effective nuclear charge. This is the true nuclear charge minus the shielding effect of the other electrons.
Hydrogen and hydrogenic ions can have their exact wave functions Ψ found using the Schrödinger equation. From Ψ and Ψ2 we obtain the information we need to fully characterize and visualize electron orbitals in their hydrogenic forms: s, p, d, f, etc.
An exact solution to the Schrödinger equation for situations involving two or more electrons is not achievable. All of the electrons are governed by a single multi-electron wave function that cannot be written as an analytic mathematical function - the mathematics involved is too hard.
Computers can provide a numerical solution for a multi-electron wave function using principles such as the variation theorem. Although such solutions are valuable in terms of characterizing electron behavior, they do not provide information suitable for visualizing electron orbitals.
We write the true multi-electron wave function Ψ as the product of the single-electron wave functions for all the electrons in the system:
For example, the wave function of a lithium atom would be written:
We obtain each of the single-electron wave functions by considering each electron in turn and basing our calculations on how the electron interacts with the effective nuclear charge.
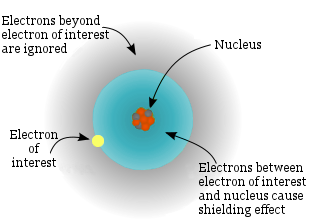
Effective Nuclear Charge
The electrons are regarded as having a spherical distribution around the central nucleus. The math is simplified by making the assumption that each electron feels the attraction of a positive point charge (the nucleus) and repulsion from the average charge distribution of all the other electrons. i.e. individual electron-electron interactions need not be calculated.
The average repulsive electric field from all the other electrons on the electron of interest is modeled as a point negative charge at the nucleus. This reduces the attraction the electron of interest feels towards the positive nuclear charge to a lower value; this lower value is described as the effective nuclear charge or shielded nuclear charge.
Zeff is the effective number of protons
Z is the number of protons
S is the number of electrons between the electron of interest and the nucleus
Using this approach the atomic orbital problem is simplified sufficiently to allow an exact wave function to be determined and orbitals visualized.
Effective Nuclear Charges for Selected Atoms
| Atom | Sublevel | Z | Zeff |
|---|---|---|---|
| H | 1s | 1 | 1 |
| He | 1s | 2 | 1.69 |
| Li | 1s, 2s | 3 | 2.69, 1.28 |
| Be | 1s, 2s | 4 | 3.68, 1.91 |
| B | 1s, 2s, 2p | 5 | 4.68, 2.58, 2.42 |
| F | 1s, 2s, 2p | 9 | 8.65, 5.13, 5.10 |
| Na | 1s, 2s, 2p, 3s | 11 | 10.63, 6.57, 6.80, 2.51 |
Table Data from E. Clementi and D. L. Raimondi; The Journal of Chemical Physics 38, 2686 (1963).
