Orbital nodes refer to places where the quantum mechanical wave function Ψ and its square Ψ2 change phase. Since the phase is either moving from positive to negative or vice versa, both Ψ and Ψ2 are zero at nodes.
Where Ψ2 is zero, the electron density is zero. Hence, at a node, the electron density is zero.
Nodes may be classed as radial, or angular.
What is a Node?
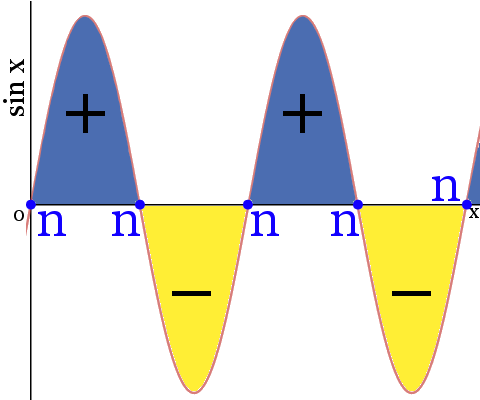
Consider the sine function sin x as a simple wave function Ψ. The diagram below shows:
- when sin x is greater than zero, the phase of the wave is positive
- when sin x is less than zero, the phase of the wave is negative
- when sin x is zero, the point is described as a node
Now consider sin2 x, the square of the original function. In quantum chemistry Ψ2 provides us with the electron density - it defines the size and shapes of the familiar orbitals s, p, d, f, etc.
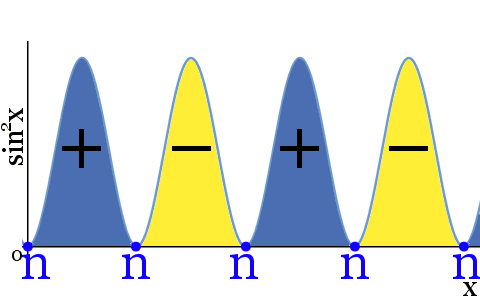
The diagram above shows:
- sin2 x has identical nodes to sin x
- the value of sin2 x has no negative values
- where the phase of Ψ was positive the phase of Ψ2 is still positive
- where the phase of Ψ was negative the phase of Ψ2 is still negative
- nodes separate positive and negative phases
Note on Phase and Nodes
Even though Ψ2 has no negative values,
in quantum mechanics the phase information carried by the original function Ψ is not lost.
For this reason the graph of sin2 x above is shown with positive and negative phases matching with the positive and negative phases of the original sin x.
Many real orbitals, such as 2s, 2p, and 3d orbitals have regions with both positive and negative phase. These regions are separated by nodes.
For example, the diagrams below show 1s, 2s, and 3s orbitals. Notice how the 2s and 3s orbitals have radial nodes separating different phases.
1s 2s

The 1s orbital has no nodes; the entire orbital is the same phase. The 2s orbital is larger, and has one radial node separating two phases.
3s
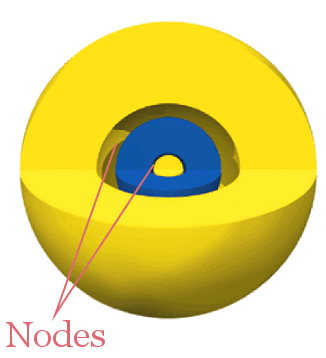
The 3s orbital has two radial nodes separating three phases.
Orbital Diagrams
2px

2py

2pz

All the 2p orbitals have a single angular node, a plane, separating the positive and negative phases of the orbitals. This is shown below in gray.
2px

2py
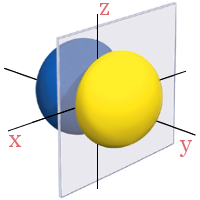
2pz
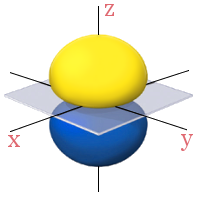
3d Orbitals
All the 3d orbitals have two angular nodes. In four of the orbitals, these nodes are planes separating the positive and negative phases of the orbitals. In the fifth orbital, the nodes are two conical surfaces.
3dxy
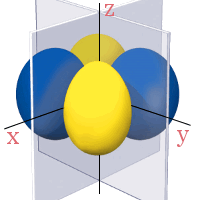
3dxz
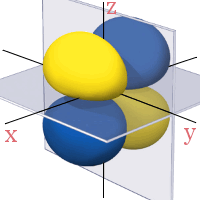
3dyz
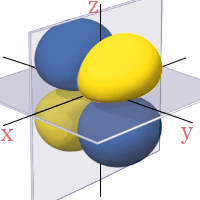
3dx2 - z2
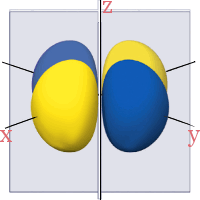
3dz2
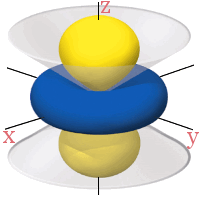

Orbital Nodes
Number of Nodes
As you might have noticed in the orbitals above, the number of nodes in an orbital follows a rule.
The number of nodes is always one less than the principal quantum number: Nodes = n - 1.
- In the first electron shell, n = 1. The 1s orbital has no nodes.
- In the second electron shell, n = 2. The 2s and 2p orbitals have one node.
- In the third electron shell, n = 3. The 3s, 3p, and 3d orbitals have two nodes, etc.
Types of Node
There are two types of node: radial and angular.
- The number of angular nodes is always equal to the orbital angular momentum quantum number, l.
- The number of radial nodes = total number of nodes minus number of angular nodes = (n-1) - l
Node Calculation Examples
Second Shell
In the second electron shell, the 2s orbital has n=2 and l=0. The number of angular nodes = l = 0. The number of radial nodes = [(n-1) - l] = [1 - 0] = 1
In the second electron shell, the 2p orbital has n=2 and l=1. The number of angular nodes = l = 1. The number of radial nodes = [(n-1) - l] = [1 - 1] = 0
Third Shell
In the third electron shell, the 3s orbital has n=3 and l=0. The number of angular nodes = l = 0. The number of radial nodes = [(n-1) - l] = [2 - 0] = 2
In the third electron shell, the 3p orbital has n=3 and l=1. The number of angular nodes = l = 1. The number of radial nodes = [(n-1) - l] = [2 - 1] = 1
In the third electron shell, the 3d orbital has n=3 and l=2. The number of angular nodes = l = 2. The number of radial nodes = [(n-1) - l] = [2 - 2] = 0
The Significance of Phases - Constructive & Destructive Interference
The fact that the phase of electron orbitals can be positive or negative is hugely significant for chemistry.
When orbitals interact, those with like sign phases interfere constructively. Those with unalike signs interfere destructively.
An example of this is orbital hybridization.
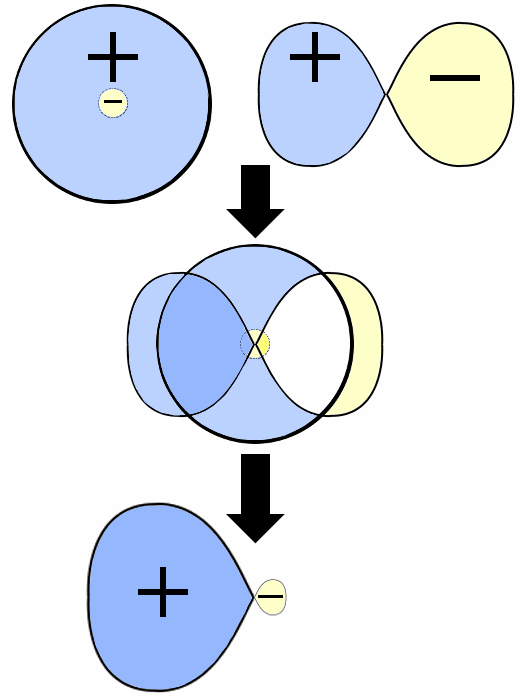
Orbital Hybridization
Orbital hybridization is fundamental to understanding organic chemistry. When an s orbital and a p orbital hybridize, the orbital phases are crucial. This is summed up in the following diagram, where a positive phase 2s orbital and a 2p orbital interact to produce an sp hybrid orbital.
Creative Commons
Figures 3, 5, and 6 based on orbital diagrams originally prepared and courtesy of UCDavis Chemwiki, CC BY-NC-SA 3.0 US.
