Redox Reactions
Redox stands for reduction-oxidation. A gain of electrons is a reduction. A loss of electrons is an oxidation.
The equations above are half-equations. The whole equation for a redox reaction is obtained by adding the half-equations.
The Redox Potential
If the reactants in a redox reaction are mixed in the same vessel, they will produce products in the same vessel - reduction and oxidation occur in the same vessel.

However, the reactants can be split in an electrochemical cell, so that the reduction and oxidations reactions occur separately. This allows us to find their individual contributions to the reaction, including Gibbs free energies.
The redox potential is an electric potential measured in volts.
Since 1 volt is identical to 1 joule per coulomb, at the atomic level the redox potential can be considered to measure the energy change per electron transferred.
The redox potential of a half-reaction is measured versus a reference electrode half-reaction whose redox potential is assigned a value of 0 volts.
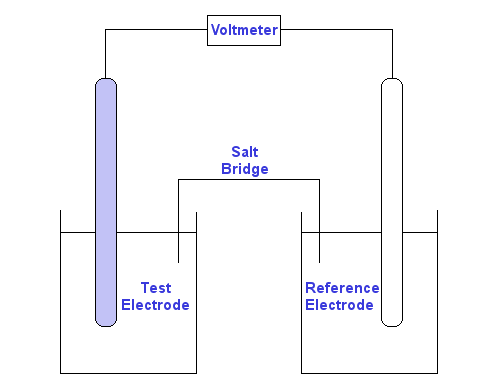
of a half-reaction compared with a known half-reaction.
Redox potential is given the sign E. If it is a standard redox potential, it is given the sign Eo.
Writing the Redox Potential
Redox potentials are measured for half-reactions. By convention they are always written as reductions, even for oxidation reactions. Half-cells that undergo reduction are assigned positive potentials, while those that undergo oxidation are assigned negative potentials.
For example, the standard redox potential for fluorine, which has a very high affinity for electrons, is positive. The standard redox potential for lithium, which loses electrons, is negative. Note how the lithium reaction is written as a reduction.
Positive Redox Potentials
Positive redox potentials indicate the reaction tends to proceed from left to right. The higher the value, the greater the tendency. Here are three examples of half-reactions with positive redox potentials:
Gold ions have a high affinity for electrons and hence are easily reduced back to metallic gold.
Negative Redox PotentialsNegative redox potentials indicate the reaction tends to proceed from right to left; the higher the absolute value, the greater the tendency. Here are three examples of half-reactions with negative redox potentials:
E tells you what will be Reduced or Oxidized
You can use E or Eo values to predict the outcome of a redox reaction. This works well whether the reaction is an electrochemical reaction in two half-cells or a chemical reaction in a single vessel.
In general, the half-equation with the more positive redox potential will be the reduction reaction and the other will be the oxidation.
Example 1
If we had two half-cells with the above species, F2(g) will be reduced and Cl- oxidized.
Example 2
If we had two half-cells with the above species, Al3+ will be reduced and Li oxidized.
Example 3
If we had two half-cells with the above species, Cl2(g) will be reduced and Mg oxidized.
Calculating the Overall Cell Potential
To find the total electric potential of any electrochemical cell we use this equation:
In electrochemical cells, reduction takes place at the cathode and oxidation at the anode, so we could alternatively write:
We can now apply this equation to the half-reactions in the three examples above to calculate the voltage of the cells:
Example 1
Example 2
Example 3
Calculating the Gibbs Free Energy, ΔG
E can also be used to calculate the Gibbs free energy ΔG for a half-reaction or reaction using the equation:
where n is the number of moles of electrons transferred in the half-reaction equation and F is the Faraday constant.
For a reaction to proceed spontaneously, ΔG must have a negative value. Therefore reactions proceed spontaneously for cells and half-cells with positive values of E.
