What is a Lattice?
A lattice is an ordered array of points describing the arrangement of particles that form a crystal.
The unit cell of a crystal is defined by the lattice points. The unit cell is the smallest part of a crystal that repeated regularly through translation in three dimensions creates the whole crystal.
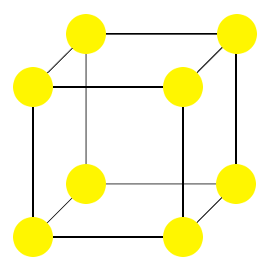
For example, the image shown here is the unit cell of a primitive cubic structure.
In the structure drawn, all of the particles (yellow) are the same. In this particular case, the lattice points defining the unit cell coincide with the centers of the crystal's particles. This need not always be the case.
The Ionic Lattice
If a crystal is formed of ions, the compound can be described as an ionic lattice.
Well-known examples of ionic lattices are sodium chloride, potassium permanganate, borax (sodium borate) and copper(II) sulfate.

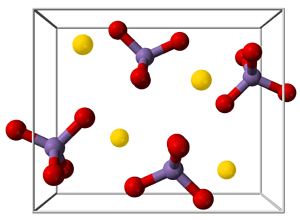
The Covalent Lattice
If a crystal is made up of covalently bonded atoms, it can be described as a covalent lattice or infinite covalent lattice.
Well-known examples of covalent lattices are diamond, quartz (silicon dioxide), silicon, and grey tin.
Lattice Constants
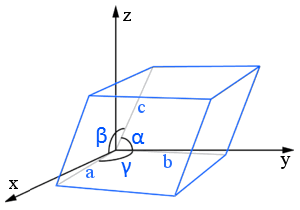
The lattice constants (or lattice parameters) are the lengths and the angles between of the edges of the unit cell.
In this parallelepiped lattice diagram, the lattice constants are a, b, and c (lengths) and α, β, and γ (angles).
Lattice Structures
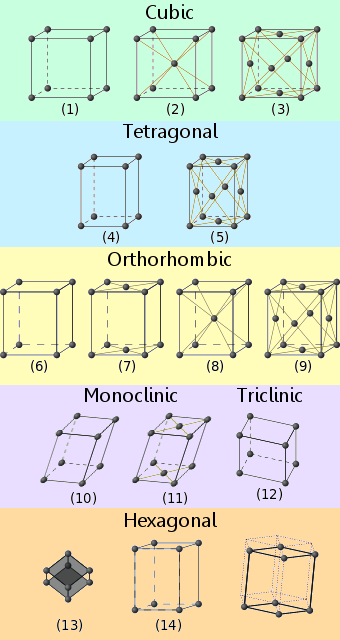
Crystalline materials fit into one of fourteen recognized lattice arrangements. These are known as Bravais lattices.
The names of the crystal lattice systems, corresponding to the numbers on the diagrams, are as follows:
1. Primitive cubic
2. Body centered cubic
3. Face centered cubic
4. Primitive tetragonal
5. Body centered tetragonal
6. Primitive orthorhombic
7. Base centered orthorhombic
8. Body centered Orthorhombic
9. Face centered Orthorhombic
10. Primitive monoclinic
11. Base centered monoclinic
12. Triclinic
13. Rhombohedral
14. Hexagonal
Lattice Defects
If a crystal were assumed to be based on a mathematically perfect ionic lattice, its calculated tensile strength would be much greater than is actually observed.
Real crystals have lattice defects that are sources of weakness. Ions missing from their expected locations and ions occupying unusual coordination sites are examples of lattice defects.
Lattice defects can also be beneficial, improving the conductivity of some semiconductor materials, for example.
