Confidence limits are calculated from experimental data and operate in tandem with a percentage confidence level.
For example, the average value of a set of pH measurements on a particular acid might be 1.4.
Statistical analysis (discussed below) of the data from which the average was calculated allows confidence limits to be placed on this average.
Let us assume statistical analysis indicates there is a 99 percent probability that the true value of the pH is 1.4 ± 0.2; then we can say that the confidence limits for the pH value are 1.2 and 1.6, and with 99% confidence that the true pH is between 1.2 and 1.6.
To calculate confidence limits, we need to know about the precision of our average value.
To find this, we first calculate the standard deviation, s, of the data. Standard deviation is calculated from:
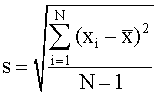
where:
N is the number of measurements
xi is each individual measurement
is the mean of all measurements
The quantity (xi - ) is called the "residual" or the
"deviation from the mean" for each measurement.
The quantity (N - 1) is called the "degrees of freedom" for the measurement.
Once we know the average (mean) and the standard deviation, we can calculate confidence limits:
The confidence interval μ is calculated from the standard deviation using:
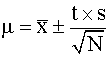
The value of t is taken from a statistical table for the number of degrees of freedom and the degree of confidence desired.
The confidence limits are the two values resulting from calculating the confidence interval.